Giáo dục

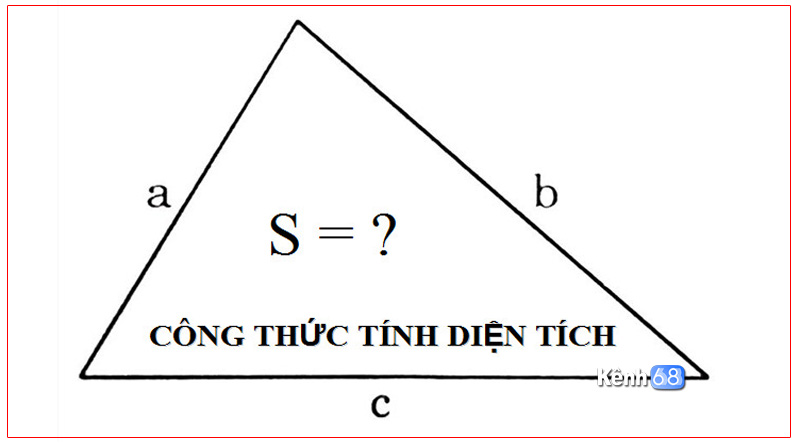
Công thức tính diện tích tam giác thường, vuông, cân, đều, đầy đủ

Bởi

15 Tháng Năm, 2019

244

Để có thể tính diện tích tam giác chúng ta có nhiều cách cũng như áp dụng nhiều công thức tính diện tích tam giác khác nhau và tất nhiên những công thức đó đều đã được chứng minh là đúng. Trong bài viết này Kenh68.net xin được chia sẻ tới các bạn học sinh tổng hợp những công thức cách tính diện tích tam giác của các loại tam giác thường gặp.

Mục lục nội dung

Các loại tam giác thường gặp

Trong quá trình học các bạn sẽ thường gặp các loại tam giác như:

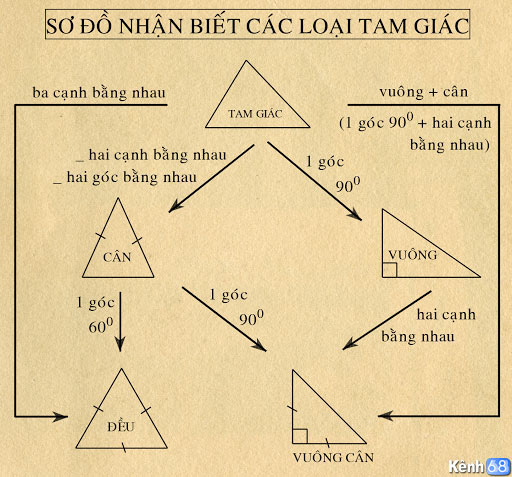
Sơ đồ nhận biết các loại tam giác – Nguồn: Internet

Tam giác thường: Là tam giác có độ dài 3 cạnh khác nhau, các góc trong cũng khác nhau
Tam giác đều: Đây có thể nói là trường hợp đặc biệt của tam giác cân. Tam giác đều là tam giác có 3 cạnh bằng nhau, đồng thời các góc trong cũng bằng nhau và bằng 60 độ.
Tam giác cân: Là tam giác có 2 cạnh bất kỳ bằng nhau được gọi là 2 cạnh bên. Hai cạnh này chung nhau đỉnh nào thì tam giác cân tại đỉnh đó, 2 góc còn lại của tam giác cân được gọi là góc đáy và chúng bằng nhau.
Tam giác vuông: Là tam giác có 1 góc bất kỳ = 90 độ góc này sẽ được gọi là góc vuông. Cạnh đối diện với góc vuông được gọi là cạnh huyền (là cạnh lớn nhất trong tam giác vuông). Hai cạnh còn lại được gọi là 2 cạnh góc vuông
Tam giác nhọn: Là tam giác có 3 góc trong đều < 90 độ
Tam giác tù: Là tam giác có 1 góc trong > 90 độ.

>>> Đọc thêm: Các tháng trong tiếng anh

Tổng hợp công thức tính diện tích tam giác

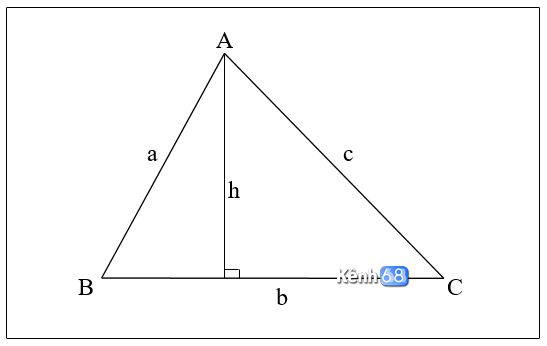
Cách tính diện tích tam giác thường, phổ biến

Cách tính diện tích tam giác phổ biến được áp dụng nhiều và cho hầu hết các loại tam giác vuông, cân, đều đó là:

$S_{ABC}=\frac{1}{2}a.h_a=\frac{1}{2}b.h_b=\frac{1}{2}c.h_c$

Trong đó:

S là diện tích tam giác
a hoặc b hoặc c là chiều dài đáy tam giác
h là chiều cao của tam giác ứng với phần đáy chiếu lên

Diễn giải: Diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài đáy. Sau đó đem tất cả chia cho 2.

Cách tính diện tích tam giác khi biết 1 góc và 2 cạnh kề

Khi một tam giác mà bạn biết được 2 cạnh và góc tạo bởi 2 cạnh đó thì lúc này chúng ta có thể áp dụng công thức tính diện tích tam giác như sau:

$S_{ABC}=\frac{1}{2}a.b.sinC=\frac{1}{2}a.c.sinB=\frac{1}{2}b.c.sinA$

Trong đó:

S là diện tích tam giác
a, b, c là độ dài các cạnh của tam giác
A, B, C là các góc của tam giác

Diễn giải: Diện tích tam giác bằng 1 phần 2 tích của 2 cạnh và sin của góc hợp bởi 2 cạnh đó trong tam giác

Cách tính diện tích tam giác khi biết 3 cạnh

Trong trường hợp bạn không xác định được chiều cao của tam giác nhưng lại biết được độ dài 3 cạnh của tam giác đó thì chúng ta có thể áp dụng công thức Heron như sau:

$S=_{ABC}=\sqrt{p(p-a)(p-b)(p-c)}$

Trong đó:

p là chu vi của tam giác
a, b, c lần lượt là độ dài các cạnh của tam giác

Công thức tính diện tích tam giác vuông

Tam giác vuông có thể coi là một trường hợp đặc biệt của tam giác khi có 2 cạnh vuông góc với nhau.

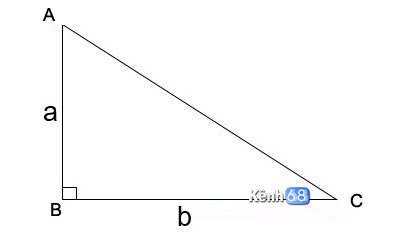
Để tính diện tích tam giác vuông ngoài việc bạn có thể áp dụng công thức tính ở trên, chúng ta có thể sử dụng một công thức riêng biệt cho tam giác vuông như sau:

$S_{ABC}=\frac{1}{2}a.b$

Trong đó: a, b là độ dài 2 cạnh góc vuông của tam giác

Cách tính diện tích tam giác cân

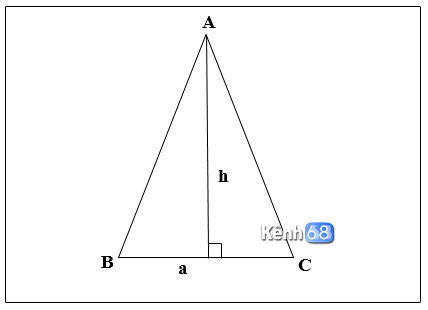
Tam giác cân tuy cũng là một trường hợp đặc biệt của tam giác bởi có 2 cạnh bằng nhau nhưng lại không có công thức tính diện tích riêng biệt. Do đó chúng ta có thể sử dụng bất kỳ cách tính diện tích tam giác nào được chia sẻ ở trên. Ví dụ ta có thể áp dụng công thức:

$S_{ABC}= \frac{1}{2}a.h_a$

Trong đó:

a là chiều dài cạnh đáy
h là chiều cao của tam giác ứng với phần đáy chiếu lên

Cách tính diện tích tam giác đều

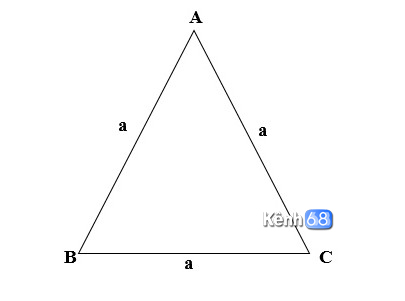
Tam giác đều cũng là một trường hợp đặc biệt của tam giác khi nó có 3 cạnh bằng nhau. Ngoài việc có thể áp dụng những công thức tính thông thường ở trên, tam giác đều cũng sẽ có cách tính diện tích riêng biệt như sau:

$S_{ABC}=a^2.\frac{\sqrt{3}}{4}$

Trong đó: a là độ dài cạnh của tam giác đều

Như vậy trên đây là toàn bộ chia sẻ về cách tính cũng như công thức tính diện tích tam giác. Hy vọng đây sẽ là những kiến thức có thể giúp ích được các bạn học sinh chưa nắm được cách tính diện tích tam giác hoặc muốn ôn lại kiến thức.

Khánh Khiêm | Kenh68.net